/ Články / Matematika / Narozeninový paradox

Narozeninový paradox

Pamatujete na to, když nějací dva spolužáci ve vaší školní třídě nebo kolegové na pracovišti měli narozeniny ve stejný den? Říkali jste si, že to je zajímavé a nepravděpodobné? Napadlo vás zjistit, jaká je vůbec pravděpodobnost takové události? Kolik myslíte, že potřebujete náhodně vybraných lidí v jedné místnosti, aby pravděpodobnost, že v dané skupině budou mít dva lidé narozeniny ve stejný den, byla téměř 100%? Možná vás výsledky překvapí.
Autor: Jiří Thomayer

Než začneme počítat, budou se nám hodit následující základní vlastnosti pravděpodobnosti. Jedna z nich je, že pokud spočítám pravděpodobnost opačného jevu, než který mám zadaný, pak pravděpodobnost zadaného jevu je dopočet do 1 („do sta procent“) – například pravděpodobnost, že na klasické hrací kostce „padne 6“, je 1/6 , tedy pravděpodobnost opačného jevu „nepadne 6“ je 1 – 1/6 = 5/6 . Druhou vlastností pravděpodobnosti, kterou využijeme, je samotný výpočet pravděpodobnosti. Ten se dá zjednodušit na výpočet pomocí podílu počtu „vyhovujících“ výsledků našeho jevu (označme jako k) a počtu všech možných výsledků (označme jako m) – tedy pravděpodobnost je k/m. V našem příkladu s kostkou je k = 1, protože vyhovující výsledek je jen jeden (6 se na kostce vyskytuje pouze jednou). A počet všech možných výsledků m = 6, protože na kostce se vyskytuje 6 čísel. Poslední užitečná vlastnost je, že pokud počítáme pravděpodobnost „po částech“ (tedy rozdělíme náš zkoumaný jev na více podjevů*[1]), pravděpodobnost zkoumaného jevu je součinem pravděpodobností všech rozdělených jevů. Zde nebudeme zabíhat do detailů, jak a kdy to funguje. Dostali bychom se až k podmíněným pravděpodobnostem a jejich vlastnostem, což pro účely pochopení narozeninového paradoxu nebude nutné.

Začněme s tím, že se potkáme s třemi přáteli na večeři, jsme tedy celkem čtyři. Jaká je pravděpodobnost, že alespoň někteří dva z nás budou mít narozeniny ve stejný den?

Zde již začneme využívat jednotlivé vlastnosti, čímž úlohu značně zjednodušíme. Podle první vlastnosti můžeme nejprve spočítat pravděpodobnost, že nikdo z nás nemá narozeniny ve stejný den, a později dopočtem do jedničky zjistíme pravděpodobnost, že alespoň dva z nás mají narozeniny ve stejný den. To, řečeno trochu specifičtěji, znamená, že si můžeme opačný jev rozdělit na čtyři podjevy:

  1. první člen naší skupiny (je jedno, kterým začneme) se narodil kdykoli
  2. druhý se musel narodit kterýkoli den kromě dne, kdy se narodil první
  3. třetí se musel narodit kterýkoli den kromě narozeninových dnů prvních dvou členů
  4. a konečně čtvrtý člen nesmí mít narozeniny ani v jednom ze tří předešlých dnů

Pokusíme-li se tento specifický popis nyní popsat matematicky, dostaneme pomocí druhé vlastnosti, že:

  1. první člen se mohl narodit kterýkoli z 365 dnů v roce – tedy pravděpodobnost, že se tak stane, je 365/365*[2] = 1 (to nám říká, že se někdy musel narodit, což asi nikoho nepřekvapí)
  2. druhý se mohl narodit pouze ve zbývajících 364 dnech, tedy pravděpodobnost, že se tak stane, je 364/365
  3. třetí se potom nesměl narodit v den narozenin 1. nebo 2. člena, a zbývá tedy na něj pouze 363 dní, ve kterých se narodit směl – pravděpodobnost 363/365
  4. poslední má pravděpodobnost podle stejného schématu 362/365

Nyní pomocí třetí vlastnosti „počítání po částech“ vynásobíme tyto čtyři spočtené pravděpodobnosti, čímž zjistíme pravděpodobnost opačného jevu „nikdo z nás nemá narozeniny ve stejný den“:

365/365 * 364/365 * 363/365 * 362/365 ≅ 98,4 %

A konečně tedy pravděpodobnost našeho zadaného jevu, že alespoň dva z nás mají narozeniny ve stejný den, je 1,6 % (100 % – 98,4 % – dopočet do sta procent). Asi nikoho nepřekvapí, že vyšla takto malá pravděpodobnost. Za domácí cvičení si můžete stejným způsobem zkusit spočítat pravděpodobnost stejného jevu v případě, že by se nás k večeři sešlo celkem 6 lidí (pro zvídavé výsledek je 4 %).

Pojďme si nyní pohrát s jinou myšlenkou. Kolik náhodně vybraných lidí potřebujeme umístit do jedné místnosti, aby námi zkoumaná pravděpodobnost, že alespoň dva lidé mají narozeniny ve stejný den, byla alespoň 50 %?

Kolik lidí byste hádali vy? 100? Nebo 200? Nebo myslíte, že 50 lidí by už stačilo? Jak to spočítat, víceméně už víme, využijeme úplně stejný postup jako v předešlém případě. Označme si nyní pouze počet neznámých lidí, který hledáme, jako n. Pro opačný jev „nikdo nemá narozeniny ve stejný den“ dostaneme následující výpočet:

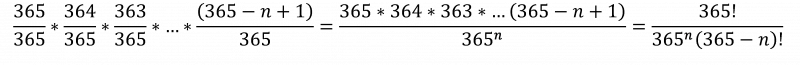
Rovnice

n = 1, 2, 3, …, 366 a ! značí faktoriál čísla*[3]

Pokud bychom za n dosadili nyní 4, dostaneme výsledek z minulého příkladu – můžeme si snadno ověřit:

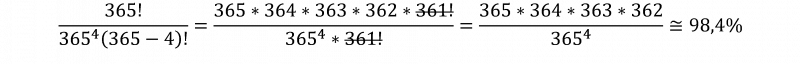
Rovnice

Jelikož hledáme odpověď, kdy pravděpodobnost pro jev „alespoň dva lidé mají narozeniny ve stejný den“ je alespoň 50 %, opačný jev musí mít menší pravděpodobnost než 50 %. A to je to, co teď budeme hledat. Tedy jakou hodnotu dosadit za n, aby vztah výše dal hodnotu menší než 50%, přičemž budeme hledat nejmenší takové číslo, u kterého to platí. Najít totiž jakékoli není těžké, můžeme jednoduše vzít n = 366 -> tímto dostaneme pravděpodobnost rovnou přesně 0 %. Což je logické, protože budeme-li mít 366 lidí, tak i kdyby 365 z nich mělo narozeniny každý v jednom dni v roce, pak již ten 366. člověk musí mít zákonitě narozeniny jako jeden z těch 365 lidí (připomínám, že se nebere do úvahy přestupný rok). Tedy pravděpodobnost, že nikdo z 366 lidí nemá narozeniny ve stejný den, je nulová. Pojďme tedy hledat ono nejmenší n – zkusíme dosadit 100, které jsme hádali zpočátku. Tím dostaneme hodnotu 0,00003 %. Wow, to je hodně malá pravděpodobnost, co? Bude tedy potřeba rozhodně hledat nějaké číslo menší – zkusme například 50. Po dosazení dostaneme 2,96 %. Jak je to možné, že tak málo? Dobře, nebudu vás dlouho napínat. Po chvilce hádání a počítání byste dospěli až k číslu 23, které když dosadíme do vztahu, dostaneme pravděpodobnost 49,27 %. Z toho plyne, že pravděpodobnost hledaného jevu, že alespoň dva lidé ve skupině 23 lidí mají narozeniny ve stejný den, je rovna 50,73 %, což bylo to, co jsme hledali. Je možné, že v takto malé skupině 23 lidí už je to padesát na padesát, že alespoň dva lidé sdílí stejný den narozenin? Ano je, a je to dáno tím, že se nesoustředíme na jednoho člověka ve skupině, jehož den narození porovnáváme s ostatními, nýbrž porovnáváme narozeniny veškerých možných párů, které těchto 23 lidí tvoří.

Těchto párů je (23 * 22) / 2 = 253, což je mnohem více než polovina dní v roce. V tomto kontextu už to tak nelogicky nevypadá, že?

Na závěr bych vypíchnul ještě jedno číslo, kterým je číslo 69. Pokud ho dosadíme do vztahů výše, zjistíme, že pravděpodobnost, že mezi 69 náhodně vybranými lidmi jsou alespoň dva, kteří mají narozeniny ve stejný den, je 99,9 %. Dá se říct, že už je téměř jisté, že mezi 69 lidmi se najdou dva, co mají narozeniny ve stejný den.

Na těchto příkladech je dobře ilustrováno, že náš rozum se dokáže poměrně snadno pomýlit, pokud necháme pracovat pouze intuici. Stále si myslíte, že je to taková náhoda, když se potkají dva lidé ve školní třídě, kteří mají narozeniny ve stejný den?

*[3] Pro připomenutí faktoriál čísla x se počítá tak, že se vynásobí všechna přirozená čísla, která jsou menší než dané x. Např. 5! = 5 * 4 * 3 * 2 * 1 = 120. Faktoriál má jednu krásnou vlastnost, že takto uspořádané součinitele můžete kdykoli přestat vypisovat a za poslední z nich připsat faktoriál, aniž byste tímto postupem změnili výsledek, např. 5! = 5 * 4! = 5 * 4 * 3! = 5 * 4 * 3 * 2! = 5 * 4 * 3 * 2 * 1 = 120.

*[2] V celém článku jsme počítali s předpokladem, že se lidé rodí během roku rovnoměrně a nezávisle na sobě a že neexistuje přestupný rok. Je to sice mírné zjednodušení, které ale na myšlence nic nekazí.

*[1] Vybrané podjevy musí mít tu vlastnost, že náš zkoumaný jev je totožný s tím, že nastanou všechny podjevy současně.